In preparing for my talk about Drupal's search capabilities I've been looking at all sorts of interesting things. One of them is Zipf's Law, which predicts that "the frequency of any word is roughly inversely proportional to its rank in the frequency table". Since Drupal's HTML indexer normalizes the word scores on the assumption that this is true, I thought it would be interesting to see whether the words in Drupal.org's index actually fall into a Zipf-like distribution. For example, in the Drupal.org search index, the word the is the most common (as it is in the English language in general), occurring 120,306 times out of 11,182,265 (1%)*. Zipf's law predicts that the second most common word (and in the case of Drupal.org) will occur 1/2 as frequently. As the data below shows, this is not the case.
* By default, the HTML indexer drops words shorter than 3 letters which means common English words such as a, it and an will not be indexed. Furthermore, the Drupal.org search index is full of terms (such as chx, killes and rtfm) which are not English words at all. Both of these factors influence the distribution.
To generate the frequency data, I obtained a copy of Drupal.org's search_index table and ran the following queries to calculate the count and rank of the words:
SELECT @m:=0;
SELECT @m:=@m+1 AS rank, count(word) AS count FROM search_index GROUP BY word ORDER BY count DESC;
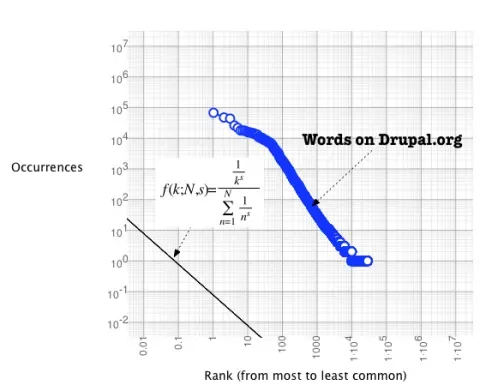
I then used the application Grapher.app to generate a pure Zipf curve as well as map the points from Drupal.org's index. Here is the result:
Zipf's law and the words (frequency/rank) of the Drupal.org search index.
The X and Y axes are both logarithmic which makes both curves appear more or less as straight lines. The slope of the Drupal.org line is not -1, and in fact, it changes along the way. Nonetheless, it shows that the search index follows some sort of inverse rank distribution, and Zipf is likely a close fit.
The graph could be made to be much nicer (for example by actually interpolating the Zipf equation on top of the Drupal.org data), but this was my first use of the Grapher.app, and I still have many things to learn about it.
Top words on Drupal.org
Below is a list of the top 20 words (out of 276046) in the search index on Drupal.org and their frequency.
RankCountWord1120306the2100101and391714for487627drupal584658thi673740that773558with872421modul967653not1067338have1165356but1258015you1357437can1452618page1549019from1648498work1747842how1847406user1947394site2046835there
Some of the words show evidence of stemming (via the Porter Stemmer module), which is the practice of taking words like module and modules and reducing both of them to modul, which is the common stem that they both share.
Calling all math-heads!
Here is a zip file with the raw data and a basis Grapher.app file with Zipf's law. If you have skills doing scientific analysis of data, can make a better graph than I have done, or want to explore Zipf's law further, please take the data and work your magic. Please report back here with whatever you find.
If you want to get started with Zipf's law in Grapher.app, here is the text that you can paste in order to get the basis equation: f({k;N,s})=|_frac_{{|_frac_{{1};{k^{s}}}};{|_sum_{{n=1};{N};{|_frac_{{1};{n^{s}}}}}}}
Here is a LaTeX expression of the same: f\left( k;N,s \right)=\frac{\frac{1}{k^{s}}}{\sum_{n=1}^{N}{\frac{1}{n^{s}}}}